АВС - равносторонний |
| << 2 | 1 >> |
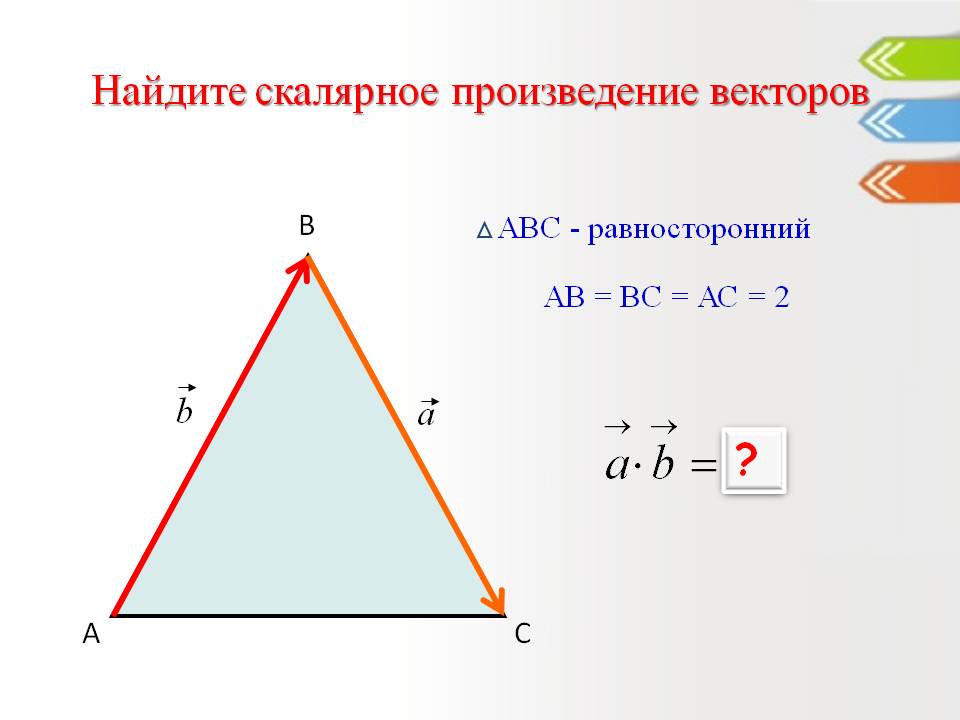
-2. Найдите скалярное произведение векторов. ? В. АВС - равносторонний. Ав = вс = ас = 2. А. С.
Скачать презентацию
Геометрия 9 класс
краткое содержание других презентаций«Действия с векторами на плоскости» - Скалярное произведение векторов. Вычитание векторов. Векторы. Неколлинеарные векторы. Угол между двумя векторами. Сложение векторов по правилу многоугольника. Умножение вектора на число. Сложение векторов. Равные векторы. Коллинеарные векторы. Метод координат.
«Центральная симметрия относительно точки» - Какие буквы имеют центр симметрии. Фигура называется симметричной относительно точки О. Точка О – центр симметрии. Центр в вершине фигуры. Центр во внутренней области фигуры. Причудливые формы в природе. Хотите увидеть больше. Центр симметрии в вершине угла. Центр симметрии принадлежит стороне угла. Центр симметрии расположен во внутренней области угла. Точки А и А1 называются симметричными относительно точки О.
««Метод координат» 9 класс» - Два противоположных луча. Докажем формулу. Абсцисса. Равнобедренный прямоугольный треугольник. Точки пересечения осей координат. Уравнение первой степени. Формула. Расстояние между точками. Координаты середины отрезка. Середина C отрезка AB. Координаты точки. Точка M1 (x1; y1) не принадлежит окружности. Координатный метод. Уравнение прямой. Воспользуемся формулой для нахождения расстояния. Найдите координаты точек.
««Зачёты по геометрии» 9 класс» - Краткая инструкция для обучающихся. Вопросы для самоподготовки. Основное тригонометрическое тождество. Метод координат. Теорема о разложении вектора. Зачеты по геометрии 9 класс. Скалярное произведение векторов. Длина окружности и площадь круга. Определение правильного многоугольника. Содержание. Определение вектора.
«Определение многоугольника» - Многоугольники. Ломанной называется фигура, образованная конечным набором отрезков. Теорема. Знатоки правил и определений. Представление и приветствие команд. Свойство углов вписанного четырехугольника. Около четырехугольника можно описать окружность. Сумма любых n несоседних углов описанного четырехугольника. Ломанная называется простой, если она не имеет точек самопересечения. Предмет. Какая ломанная называется простой.
«Построение сечений» - Сечение прямой призмы. Построить точку пересечения. Правильная шестиугольная призма. Подготовительные задачи. Алгоритм построения сечений. Задачи на построение сечений. Тетраэдр. Построение сечений. Общие точки. Сечение тетраэдра.
Всего в теме «Геометрия 9 класс» 54 презентации