Пример: х3 – 5 х2 + 8 х – 4 = 0 х3 – 2 х2 –3 х2 + 8х – 4 = 0 х2 (х – |
|
Скачать презентацию |
||
| << Решение уравнений третьей степени | Цель работы: Выявить способы решения уравнения третьей степени >> |
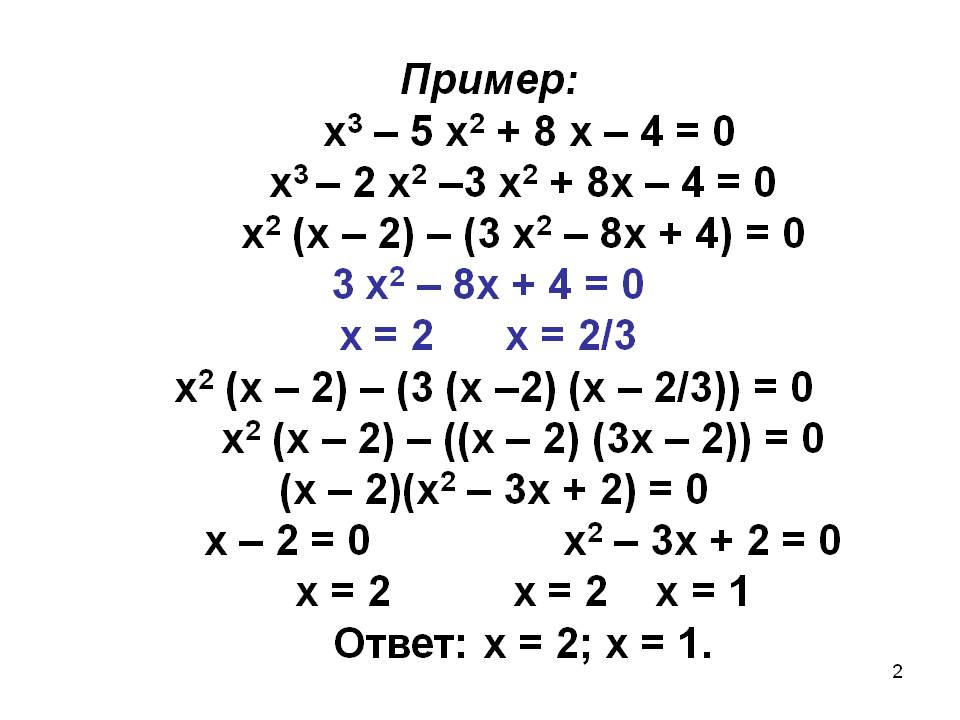
Пример: х3 – 5 х2 + 8 х – 4 = 0 х3 – 2 х2 –3 х2 + 8х – 4 = 0 х2 (х – 2) – (3 х2 – 8х + 4) = 0 3 х2 – 8х + 4 = 0 х = 2 х = 2/3 х2 (х – 2) – (3 (х –2) (х – 2/3)) = 0 х2 (х – 2) – ((х – 2) (3х – 2)) = 0 (х – 2)(х2 – 3х + 2) = 0 х – 2 = 0 х2 – 3х + 2 = 0 х = 2 х = 2 х = 1 Ответ: х = 2; х = 1. 2.
Скачать презентацию
Алгебра 11 класс
краткое содержание других презентаций«Применение определённого интеграла» - Определение объема тела. §5. Суммы Дарбу. §3. Цель: Нахождение статических моментов и центра тяжести кривой. §7. Интегральная сумма. §4. Задачи: Вводные замечания. §2. Оценка разности S-s. §6. Нахождение статических моментов и центра тяжести плоской фигуры. §8. Механическая работа. Вычисление длины кривой. §2. Методы интегрирования. §3. Свойство разности значений первообразной. §5. Свойства определенного интеграла.
«Иррациональные уравнения» - Урок по алгебре в 11 классе. Типология урока: Урок типовых задач. Развитие навыка самоконтроля, умений работать тестами. 1.Сообщение темы, цели и задач урока. 2.Проверка д/з. Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений. Основные этапы урока. Оценки за урок. На контроль. №419 (в,г),№418(в,г),№420(в,г) 3.Устная работа на повторение 4.Тест.
«Решение логарифмических неравенств» - Решите неравенство. Алгебра 11 класс. Логарифмические неравенства.
«Правила дифференцирования» - Домашнее задание. Урок по алгебре и началам анализа (11 класс) Правила дифференцирования. Каким может быть число h в отношении ? Свойства производных? Правила дифференцирования. Как называется операция нахождения производной ? Тип урока: урок повторения и обобщения полученных знаний. Вопросы: Что называется производной функции f(x) в точке x ?
«Уравнения третьей степени» - Первый пример: Здесь р = 6 и q = -2. Решение уравнений третьей степени. г.Северодвинск. Наша формула дает: Исследовательская работа. Уравнение (2) можно решить при помощи подстановки х = +. Х3 + b = ax (3). Х3 = ах + b (2). Здесь р = 6 и q =-2.Наша формула дает: 2006-2007 учебный год.
«Показательные и логарифмические неравенства» - Решение: 1.2. Решение показательных неравенств вида. 1. Показательные неравенства 1.1. Решение простейших показательных неравенств. 1.3. Решение показательных неравенств с помощью замены переменных. Лекция №5. Лекции по алгебре и началам анализа 11 класс. Сложными показательными неравенствами называются неравенства вида.
Всего в теме «Алгебра 11 класс» 35 презентаций